理論上，相同的問題應該有相同的解，但那是針對解析解而言。
實際上，所謂的CFD使用的通通都是數值解，不然也不會有什麼收斂不收斂的問題了，而數值迭代求解的起點就是給定的初始值。
也因此，可以想像的你如果猜得越準，收斂的速度就越快。

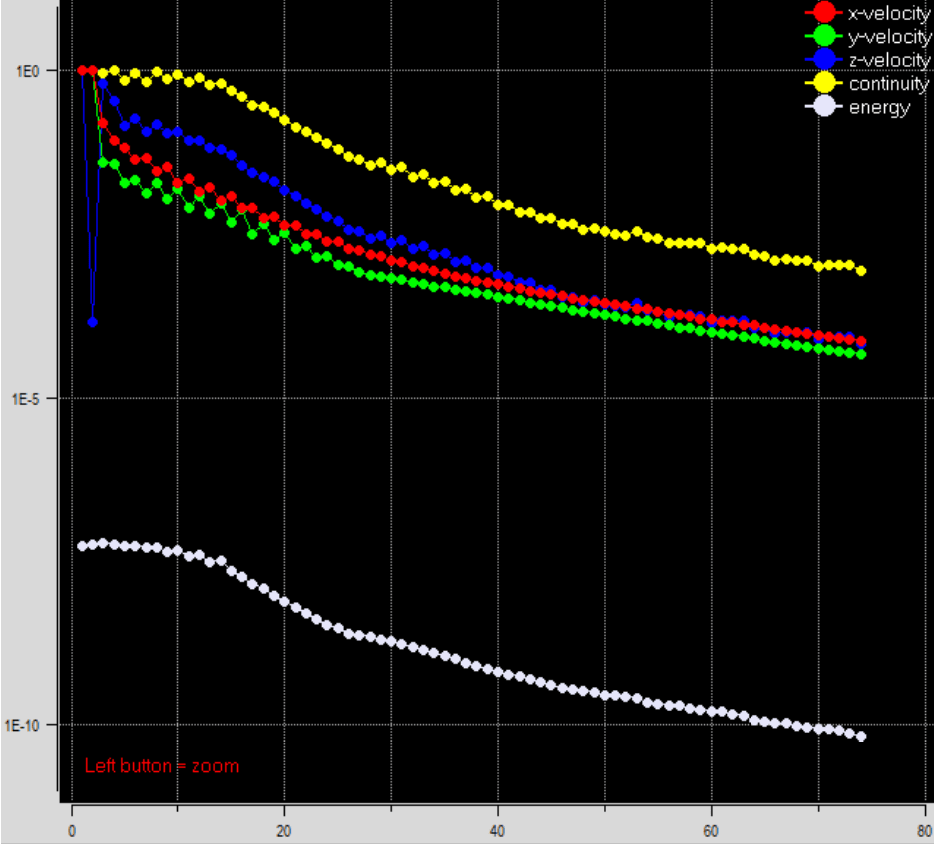
上圖是一個使用預設值，(u=0,v=0,w=0)的收斂曲線，經過了74步達到收斂。同時在過程中前期花了點時間搜尋，到了25步的時候才穩定往收斂走去。

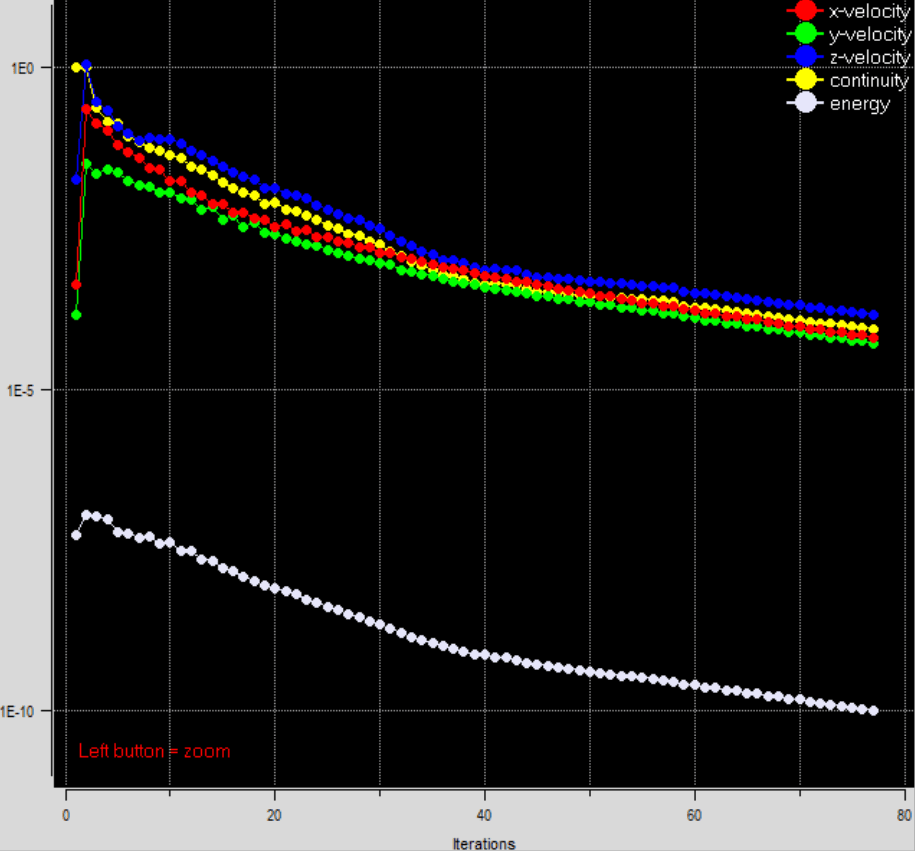
由於用來測試的問題是一個自然對流的問題，我們可以想像因為密度差，會有很多粒子是往上飄的，因此給定一個(u=0,v=0,w=0.1m/s)的初始值，結果如上圖。
基本上總步數差別並不是太大，78步。但是在前期搜尋的時候來的順利很多，並沒有像是之前25步前震盪的狀況發生。

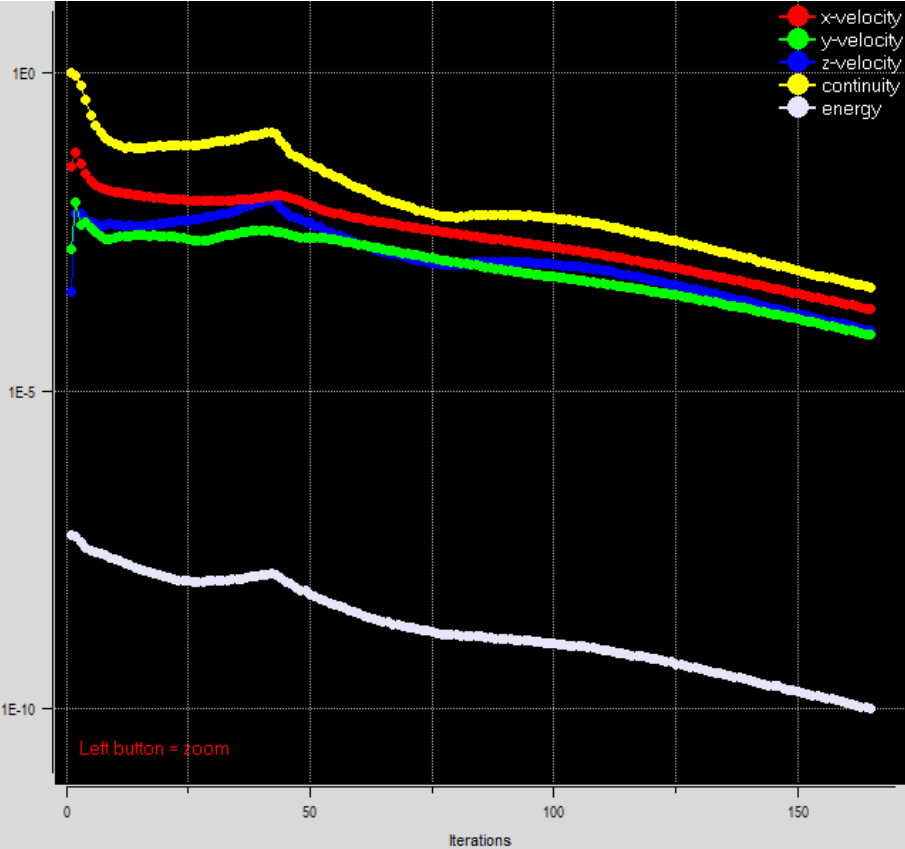
那麼如果我們沒什麼道理的給他一個初始值呢?
上圖是給定(u=0.1,v=0,w=0)的收斂曲線，很顯然的問題因為浮力的關係，w不會是0，u也因為沒有強制對流，不會有固定向的風流。結果就造成了收斂步數大幅增加到了超過150，同時在100步以前的搜尋更是辛苦。還好這是個不太困難的問題，如果是再稍微不穩定一點的問題下很可能就發散掉了。

面對一般問題，初始值造成的效果不是很明顯，但是在某些問題上是有些幫助的:
1. 給他一個好的開始能算得比較快
2. 自然對流的問題因為本來風速就很微弱，好的開始幫助問題穩定
3. 使用簡單的紊流模式所求出的解來當作複雜紊流模式的初始值幫助收斂

特別是3，有時候不這麼做甚至是難以收斂。